Conference from: ICLR 2020
Paper link: [Open Review] [PDF]
Introduction
目前的生成领域存在的一大问题就是在训练目标/损失函数/评估方法一侧,具体来说有以下几个问题:
- 暴露偏差(Exposure bias):训练时有Ground Truth输入作为矫正,而测试时没有Ground Truth,预测错误会不断累积;
- 损失函数不匹配(Loss mismatch):在训练时,最大化黄金文本的似然概率,然而在预测时,模型使用BLEU/ROUGH进行评价;
- 生成多样性不足(Generation diversity):模型倾向于生成通用的、重复的、短视的、乏味的文本;
- 负样本多样性忽略(Negative diversity ignorance):目前通用的负对数似然损失函数相当于是将不同的负样本一视同仁,和实际情况往往有出入。
以上列表中的前三个问题,目前已经有了很多的相关工作,然而第四个(负样本多样性忽略)则少有人问津。本文就旨在解决生成领域的“负样本多样性被忽略”这一问题。
目前,自然语言生成任务采用的模型一般有:seq2seq、GANs、VAE、自回归网络等,它们一般都将生成任务建模成一个序列预测任务,使用标准的最大似然估计(Maximum Likelihood Estimation,MLE)损失函数,这种损失函数通过将Ground truth的生成概率最大化(即最小化其负对数)作为损失函数进行训练:
MLE损失通过优化训练集中的黄金输出的损失,符合了经验误差最小化的原则。然而,作者认为,MLE损失仅仅将模型的所有预测输出简单地划分为正确和错误两类,忽略了正确预测和“次优”预测之间的相似性。作者认为在所有错误预测之间,也是有不同的质量级别的:有些错误预测仅仅是次优于黄金输出(比如一个词被被其同义词取代了);而另一些错误预测则是和黄金输出完全没有一点相似性。而MLE损失相当于是平等对待所有错误样本,无法精确地建模错误预测的多样性。
作者举了一个例子:armchair(扶手椅)这个词可能被误解为deskchair(书桌椅),但一般不会被误解为mashroom(蘑菇)。
Method
注:原文中使用粗体如 来表示token序列,而使用非粗体如 来表示单个token,这里的记号也和原文保持一致。
为了精确建模负样本多样性,作者采取的方法是修改传统的MLE损失函数,使之加上额外的一项目标函数 来建模负样本多样性。
作者首先引入了一个独立于模型预测的评价函数 ,使得对于黄金token 以及词表中的某个词 ,更高的 分数意味着更优(即:更贴近黄金token )的预测结果 。为了不失一般性,作者强调了这里的 也可以包含隐变量或是额外的监督信息(不过作者的方法里并没有包含,见后文)。
随后,作者引入了一个先验分布 。对于每一个目标词 ,都有一个唯一确定的分布 与之对应,该分布是从训练语料中导出的(具体见后文)。目标是让模型预测分布 符合该先验分布 ,作者使用了KL散度作为损失。同时考虑评价函数 f(\tilde{\boldsymbol{y}}, \boldsymbol{y}) 的训练,损失函数如下:
然而本文使用的方法中,分布 是从训练数据中导出的,因此独立于模型参数 (即不可训练),因此损失函数就变成了:
其中KL散度可以如下展开:
最终的训练目标如下:
其中 为平衡两项之间的超参数。
如何导出分布
分布 是从评价函数 上导出的,对于词表中的某个词 ,其先验分布 如下导出:
如何确定评价函数
作者认为对于词表中的一个特定词语 ,能够在词表的全体词语 上定义一个确切的顺序关系 ,其中 总是排第一。随后,评价函数 就可以定义为在上述顺序关系下的一个单调函数,当且仅当 时函数取得最大值。
作者直接采用预训练词向量(fastText)的余弦距离,来得到每个词语的顺序关系。
In this work, we adopt the cosine similarity of pre-trained embeddings to sort the token (word/subword) order.
最后关于函数类型,作者使用了高斯密度函数,同时也进行了其它函数的实验。然而作者在这一块并没有非常形式化的数学描述,比较含糊,因此具体的做法还有疑问。下面是来自附录的一张图:
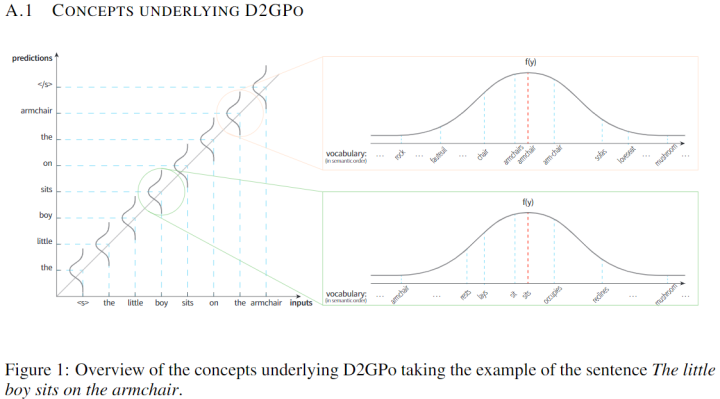
As the adopted Gaussian prior used in the training objective is derived from a data-dependent token-wise distribution, we call it the data-dependent Gaussian prior objective (D2GPo).
Experiment
作者在不同的自然语言生成任务上进行了实验,将Baseline模型与使用了本文提出的目标函数的模型相比,以证明本文提出的目标函数的效果。
Supervised NMT
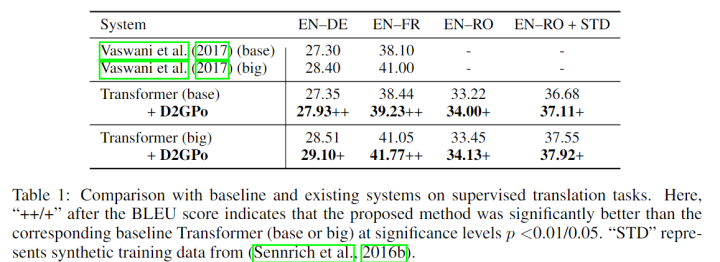
Unsupervised NMT
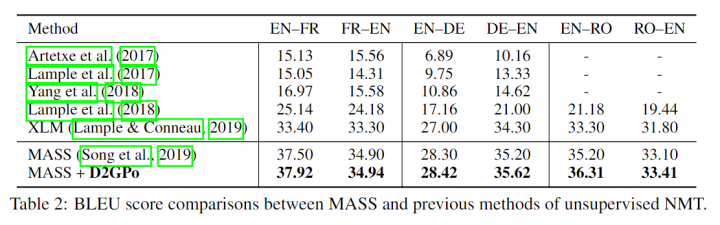
Text Summarization
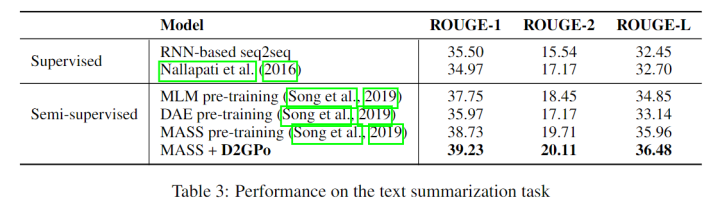
Storytelling
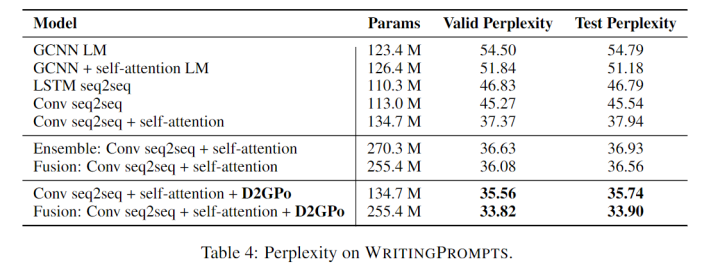
Image Captioning
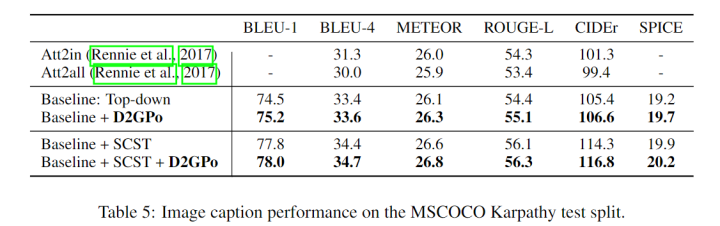
关于评价函数形式的探索
除上述生成任务外,作者也对评价函数形式进行了探索,结果高斯密度函数效果表现最好,与作者的预期相符。
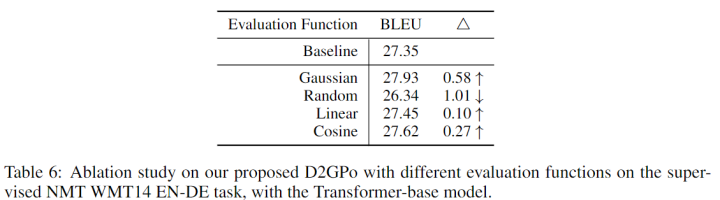
Conclusion
本文提出了文本生成领域的负样本多样性忽略问题,提出了一个新的目标函数(D2GPo)去解决该问题。在各类文本生成任务上的实验证明了本文提出方法的有效性。
